· TRABALHO ESCRITO À MÃO
· EM FOLHA DE PAPEL ALMAÇO
· DEVERÁ CONTER PARTE TEÓRICA (PESQUISA)
· DEVERÁ CONTER FIGURAS ILUSTRATIVAS DO CONTEÚDO
· EXERCÍCIOS RESOLVIDOS.
I. Análise combinatória
- Princípio multiplicativo ou princípio fundamental da contagem
- Fatorial
- Arranjos simples
- Combinação simples
- Permutação simples
- Permutação com elementos repetidos
II .
Probabilidade
- Espaço amostral
- Evento
- Cálculo da probabilidade
III. Triângulo de Pascal e o Binômio de Newton
EXERCÍCIOS RESOLVIDOS
1) De quantas maneiras 6 pessoas podem sentar-se num banco de
6 lugares de modo que duas delas fiquem sempre juntas, em qualquer ordem?
Resp:Como
duas pessoas ficarão sempre juntas, podemos considerá-las uma única pessoa.
Dessa forma temos que:
P5
= 5! = 5 . 4 . 3 . 2 . 1 = 120
Sabendo
que as duas pessoas podem se sentar de duas maneiras, teremos 2 . 120 = 240.
Portanto as 6 pessoas podem ocupar o banco de 6 lugares, em que 2 fiquem sempre
juntas, de 240 maneiras.
2)(Unifor–CE) Um
casal e seus quatro filhos vão ser colocados lado a lado para tirar uma foto.
Se todos os filhos devem ficar entre os pais, de quantos modos distintos os
seis podem posar para tirar a foto?
Resp:
Os pais deverão ocupar os extremos:
P ____ ____ ____ ____ M ou
M ____ ____ ____ ____ P
2 ..P4 = 2 . 4! = 2 . 4 . 3 . 2 . 1 =
48 maneiras
3) (UFJF–MG) Newton possui 9 livros
distintos, sendo 4 de Geometria, 2 de Álgebra e 3 de Análise. O número de
maneiras pelas quais Newton pode arrumar
esses livros em uma estante, de forma que os livros de mesmo assunto permaneçam
juntos, é:
Resp: 4 livros de Geometria =
P4
2 livros de Álgebra = P2
3 livros de Análise = P3
2 livros de Álgebra = P2
3 livros de Análise = P3
P4 . P2 . P3 . P3 = 4! . 2! . 3!
4! = 4 . 3 . 2 . 1 = 24
2! = 2
3! = 3 . 2 . 1 = 6
2! = 2
3! = 3 . 2 . 1 = 6
P4 . P2 . P3 . P3 = 24 . 2 . 6 . 6
P4 . P2 . P3 . P3 = 1728 maneiras
P4 . P2 . P3 . P3 = 1728 maneiras
Resp: O produto C6, 3 . C4, 2 = 20 . 6 = 120 nos
dá o total de pratos contendo 3 itens
de carboidrato e 2 itens
de proteína.
Já o produto C6, 2 . C4, 3 = 15 . 4 = 60 é
igual ao total de pratos contendo 2 itens
de carboidrato e 3 itens
de proteína.
Por fim o produto C6, 1 . C4, 4 = 6 . 1 = 6 resulta
no total de pratos contendo 1 item
de carboidrato e 4 itens
de proteína.
Somando 120, 60 e 6,
obtemos o mesmo resultado obtido anteriormente.
Portanto:
O
número máximo de pratos distintos que poderei fazer, contendo ao menos dois
itens de proteína, é igual a 186 pratos.
Resp: Estamos trabalhando com combinação simples, pois não importa a
ordem de preenchimento dos recipientes. No caso dos doces vamos calcular C8, 3:
Já no caso dos salgados vamos
calcular C7, 2:
O número total de combinações
será então o produto de 56 por 21:
Logo:
São
1176 as diferentes possibilidades de preenchimento do recipiente.
Como temos três tipos de
calçados, a permutação destes três tipos é igual a 6:
P3 = 3! = 3 . 2 . 1 = 6
Ou seja, estando todos os
calçados de um mesmo tipo juntos, o número de permutações é igual a 6, levando-se em consideração apenas o
tipo de calçado, mas não o calçado em si.
Para os sapatos, temos 3 deles, que permutados entre si resulta
em 6 permutações:
P3 = 3! = 3 . 2 . 1 = 6
Para os chinelos, temos 2 pares, que permutados entre si
resulta em 2 permutações:
P2 = 2! = 2 . 1 = 2
Finalmente para os tênis, temos 5 pares, que permutados entre si
resulta em 120 permutações:
P5 = 5! = 5 . 4 . 3 . 2 . 1 = 120
Multiplicando estes quatro
números temos:
P3 . P3 . P2 . P5 = 3! . 3! . 2! . 5! = 6 . 6 . 2 . 120 = 8640
As
disposições possíveis são 8640.
Resp: Quando temos apenas 1 dado, temos um total de 6 resultados possíveis.
Quando temos 2 dados, cada um dos 6 resultados possíveis de um dos
dados, pode ser combinado com cada um dos 6resultados possíveis do outro dado, resultando então em 36 resultados possíveis.
Como temos 3 dados, as 36 possibilidades combinadas dos
outros 2 dados,
combinadas às 6 possibilidades
do terceiro dado resultarão em 216 resultados.
Em outras palavras, pelo
princípio multiplicativo temos:
6 . 6 . 6 = 216
Logo:
Obteremos
um agrupamento dentre os 216 possíveis.
Resp: Para a primeira ave a subir
no poleiro tem-se 12 possibilidades,
para a segunda tem-se 11,
para a terceira tem-se 10 e
assim por diante, até a décima ave onde teremos apenas 3 possibilidades, já que apenas
duas ficarão de fora. Multiplicando tudo temos:
12 . 11 . 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 = 239500800
Resp: o espaço amostral
possui 12 elementos,
que é o número total de bolas, portanto a probabilidade de ser retirada uma
bola verde está na razão de 5 para 12.
Resp: Através do princípio fundamental da contagem podemos
determinar o número total de agrupamentos ao lançarmos três moedas.
Como cada moeda pode produzir
dois resultados distintos, três moedas irão produzir 2 . 2 . 2 resultados
distintos, ou seja, poderão produzir 8 resultados distintos. Este é o nosso espaço amostral.
Dentre as 8 possibilidades do espaço amostral,
o evento que representa todas as moedas com a mesma face para cima possui
apenas 2 possibilidades,
ou tudo cara ou tudo coroa, então a probabilidade será dada por:
A
probabilidade das três moedas caírem com a mesma face para cima é igual a 1/4,
ou 0,25, ou ainda 25%.
Resp: Sabemos que a probabilidade
da mulher engravidar em um mês é de 20%, que na forma decimal é igual a 0,2. A probabilidade dela não conseguir engravidar é igual a 1 - 0,2, ou seja, é igual a 0,8.
Este exercício trata de eventos
consecutivos e independentes (pelo menos enquanto ela não engravida), então a
probabilidade de que todos eles ocorram, é dado pelo produto de todas as
probabilidades individuais. Como a mulher só deve engravidar no quarto mês,
então a probabilidade dos três meses anteriores deve ser igual à probabilidade
dela não engravidar no mês, logo:
0,1024 multiplicado por 100% é igual a 10,24%.
Então:
A
probabilidade de a mulher vir a engravidar somente no quarto mês é de 10,24%.
Resp: Na parte teórica vimos que
a probabilidade da união de dois eventos pode
ser calculada através da fórmula e no caso da intersecção dos
eventos ser vazia, isto é, não haver elementos em comum aos dois eventos,
podemos simplesmente utilizar .
Ao somarmos a quantidade de
fichas obtemos a quantidade 14.
Esta quantidade é o número total de elementos do espaço amostral.
Neste exercício os eventos obter ficha verde e obter ficha amarela são mutuamente exclusivos, pois a ocorrência de um
impede a ocorrência do outro, não há elementos que fazem parte dos dois
eventos. Não há bolas verdes que são também amarelas.
Note que esta fórmula nada mais é
que a soma da probabilidade de cada um dos eventos.
O evento de se obter ficha verde possui 7 elementos e o espaço amostral
possui 14 elementos,
que é o número total de fichas, então a probabilidade do evento obter ficha verde ocorrer é igual
a 7/14:
Analogamente, a probabilidade do
evento obter ficha amarela,
que possui 2 elementos,
é igual a 2/14:
A
probabilidade de ela ser verde ou amarela é 9/14.
TRIÂNGULO DE PASCAL


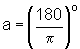 . Portanto, 1 radiano corresponde a aproximadamente 57o.
. Portanto, 1 radiano corresponde a aproximadamente 57o.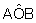 tem 1 radiano.
tem 1 radiano.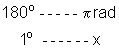
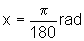 ou seja, 1o corresponde a aproximadamente a 0,017 rad.
ou seja, 1o corresponde a aproximadamente a 0,017 rad.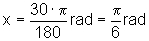
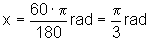
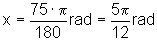
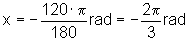
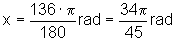
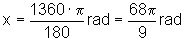
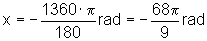
 rad,
rad, 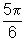 rad,
rad, 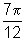 rad, 8 rad.
rad, 8 rad.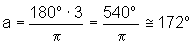
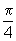 rad, temos
rad, temos 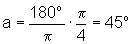
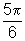 rad, temos
rad, temos 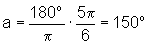
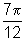 rad, temos
rad, temos 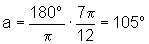
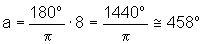
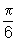 rad.
rad.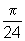 rad.
rad.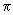 rad.
rad. rad.
rad. procurado é:
procurado é: