ATENÇÃO PARA AS DATAS.
1º BIMESTRE - entregar até 03 DE ABRIL DE 2015
2ºBIMESTRE- entregar até 09 DE JUNHO DE 2015
3ºBIMESTRE - entregar até 02 DE SETEMBRO DE 2015
4º BIMESTRE - entregar até 05 DE NOVEMBRO DE 2015.
OBS:
·
TRABALHO ESCRITO À MÃO
·
EM FOLHA DE
PAPEL ALMAÇO
·
DEVERÁ CONTER PARTE TEÓRICA (PESQUISA)
·
DEVERÁ CONTER FIGURAS ILUSTRATIVAS DO CONTEÚDO
·
EXERCÍCIOS RESOLVIDOS.
1º BIMESTRE
I. Trigonometria
- Circunferência trigonométrica
- Grau e radiano
- Arcos côngruos
- Seno
- Gráfico da função seno
- Cosseno
- Gráfico da função cosseno
- Tangente
- Gráfico da função tangente
- Cotangente
- Secante
- Cossecante
- Relações trigonométricas
EXERCÍCIOS RESOLVIDOS
1) Qual a medida, em graus, do ângulo de 1 radiano? Qual a medida, em radianos, do ângulo de 1 grau.
Logo,
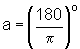. Portanto, 1 radiano corresponde a aproximadamente 57o.| O raio r é unitário; tem 1 umc. O comprimento do arco AB é 1 umc. O ângulo 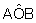 tem 1 radiano.O arco AB tem 1 radiano. |
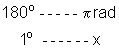
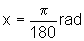ou seja, 1o corresponde a aproximadamente a 0,017 rad.2) Calcule em radianos: 30o, 60o, 75o, -120°, 136°, 1360°, -1360°.
Quando a = 30º, temos
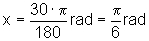
Quando a = 60º, temos
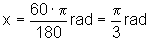
Quando a = 75º, temos
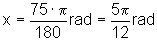
Quando a = -120º, temos
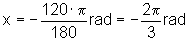
Quando a = 136º, temos
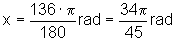
Quando a = 1360º, temos
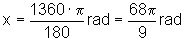
Quando a = -1360º, temos
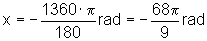
3) Calcule em graus:
3 rad,
rad, 
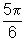rad,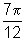 
rad, 8 rad.Quando x=3 rad, temos
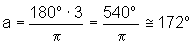
Quando x=
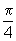rad, temos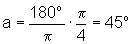 
Quando x=
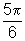rad, temos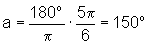 
Quando x=
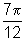rad, temos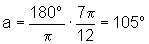 
Quando x=8 rad, temos
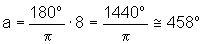
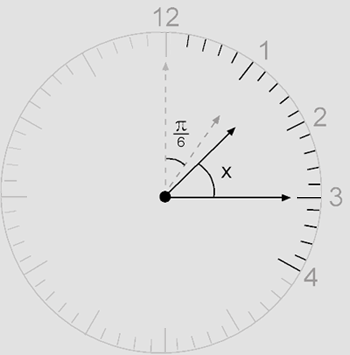
4) Calcule qual a medida em radianos do ângulo formado pelos ponteiros do relógio às 13h 15min.
O ponteiro das horas: em 1 hora, isto é, em 60 minutos, se desloca30º =
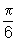rad.Então, em 15 min, o ponteiro das horas se desloca
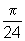rad.O ponteiro dos minutos: em 1 hora, isto é, em 60 minutos, se desloca
360º = 2
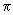rad.Então, em 15 min, o ponteiro dos minutos se desloca 90o =
rad.Portanto, em radianos, o ângulo
procurado é: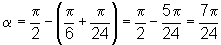
5) Calcule a primeira determinação positiva do conjunto de arcos de mesma extremidade que o arco A de medida: A= 810°
Para o arco de 810° devemos obter quantas voltas completas este arco tem pois 810°>360°. Dividindo 810 por 360, obteremos:
| 810 90 |  | 360 2 |
|---|
Este resultado significa que precisaremos dar duas voltas completas e mais 90° para completarmos o arco de 810°. Assim a primeira determinação positiva será 90°.
OBS:
·
TRABALHO ESCRITO À MÃO
·
EM FOLHA DE
PAPEL ALMAÇO
·
DEVERÁ CONTER PARTE TEÓRICA (PESQUISA) –valor 4,0
·
EXERCÍCIOS RESOLVIDOS(FOLHAS EM ANEXO).- valor 6,0
2º BIMESTRE
I. Matrizes
- Definição
- Representação genérica de uma matriz
- Matriz quadrada
- Matriz diagonal
- Matriz identidade
- Igualdade de matrizes
- Adição de matrizes
- Subtração de matrizes
- Multiplicação de um número real por uma
matriz
- Multiplicação de matriz
II.Determinantes
- Definição
- Determinante de matriz quadrada de ordem
1
- Determinante de matriz quadrada de ordem
2
- Determinante de matriz quadrada de ordem
3
III.Sistemas lineares
- Sistemas lineares 2 x 2
- Sistemas lineares 3 x 3
- Regra de Cramer
EXERCÍCIOS RESOLVIDOS
01. Obter a matriz A = (aij)2x2 definida por aij = 3 i - j.
02. Se A é uma matriz quadrada de ordem 2 e Atsua transposta, determine A, tal que A = 2 . At.
03. (UNIV. CATÓLICA DE GOIÁS) Uma matriz quadrada A é dita simétrica se A = AT e é dita anti-simétrica se AT = -A, onde AT é a matriz transposta de A. Sendo A uma matriz quadrada, classifique em verdadeira ou falsa as duas afirmações:
(01) A + AT é uma matriz simétrica
(02) A - AT é uma matriz anti-simétrica
04. Se uma matriz quadrada A é tal que At = -A, ela é chamada matriz anti-simétrica. Sabe-se que M é anti-simétrica e: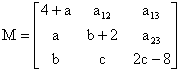
02. Se A é uma matriz quadrada de ordem 2 e Atsua transposta, determine A, tal que A = 2 . At.
03. (UNIV. CATÓLICA DE GOIÁS) Uma matriz quadrada A é dita simétrica se A = AT e é dita anti-simétrica se AT = -A, onde AT é a matriz transposta de A. Sendo A uma matriz quadrada, classifique em verdadeira ou falsa as duas afirmações:
(01) A + AT é uma matriz simétrica
(02) A - AT é uma matriz anti-simétrica
04. Se uma matriz quadrada A é tal que At = -A, ela é chamada matriz anti-simétrica. Sabe-se que M é anti-simétrica e:
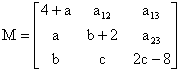
Os termos a12, a13 e a23 de M, valem respectivamente:
a) -4, -2 e 4
b) 4, 2 e -4
c) 4, -2 e -4
d) 2, -4 e 2
e) 2, 2 e 4
a) -4, -2 e 4
b) 4, 2 e -4
c) 4, -2 e -4
d) 2, -4 e 2
e) 2, 2 e 4
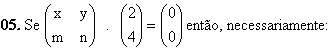
a) x = y = 0
b) x = y = m = n = 0
c) x = y e m = n
d) y = -2x e n = -2m
e) x = -2y e m = -2n
06. Na confecção de três modelos de camisas (A, B e C) são usados botões grandes (G) e pequenos (p). O número de botões por modelos é dado pela tabela:
b) x = y = m = n = 0
c) x = y e m = n
d) y = -2x e n = -2m
e) x = -2y e m = -2n
06. Na confecção de três modelos de camisas (A, B e C) são usados botões grandes (G) e pequenos (p). O número de botões por modelos é dado pela tabela:
Camisa A
|
Camisa B
|
Camisa C
| |
Botões p
|
3
|
1
|
3
|
Botões G
|
6
|
5
|
5
|
O número de camisas fabricadas, de cada modelo, nos meses de maio e junho, é dado pela tabela:
Maio
|
Junho
| |
Camisa A
|
100
|
50
|
Camisa B
|
50
|
100
|
Camisa C
|
50
|
50
|
Nestas condições, obter a tabela que dá o total de botões usados em maio e junho.
07. Sobre as sentenças:
I. O produto das matrizes A3 x 2 . B2 x 1 é uma matriz 3 x 1.
II. O produto das matrizes A5 x 4 . B5 x 2 é uma matriz 4 x 2.
III. O produto das matrizes A2 x 3 . B3 x 2 é uma matriz quadrada 2 x 2
É verdade que:
a) somente I é falsa;
b) somente II é falsa;
c) somente III é falsa;
d) somente I e III são falsas;
e) I, II e III são falsas.
08. (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.
I. O produto das matrizes A3 x 2 . B2 x 1 é uma matriz 3 x 1.
II. O produto das matrizes A5 x 4 . B5 x 2 é uma matriz 4 x 2.
III. O produto das matrizes A2 x 3 . B3 x 2 é uma matriz quadrada 2 x 2
É verdade que:
a) somente I é falsa;
b) somente II é falsa;
c) somente III é falsa;
d) somente I e III são falsas;
e) I, II e III são falsas.
08. (MACK) Se A é uma matriz 3 x 4 e B uma matriz n x m, então:
a) existe A + B se, e somente se, n = 4 e m = 3;
b) existe AB se, e somente se, n = 4 e m = 3;
c) existem AB e BA se, e somente se, n = 4 e m = 3;
d) existem, iguais, A + B e B + A se, e somente se, A = B;
e) existem, iguais, AB e BA se, e somente se, A = B.
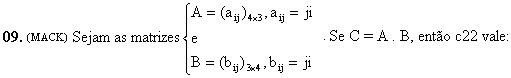
a) 3
b) 14
c) 39
d) 84
e) 258
10. (PUC) Se A, B e C são matrizes quadradas e At, Bt e Ct são suas matrizes transpostas, e igualdade falsa entre essas matrizes é:
a) (A = B) . C = A . C + B . Cb) (A + B)t = At + Bt
c) (A . B)t = At . Bt
d) (A - B)C = AC - BC
e) (At)t = A
http://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/matrizes
