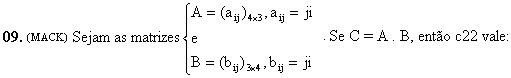OBS:
·
TRABALHO ESCRITO À MÃO
·
EM FOLHA DE PAPEL ALMAÇO
·
DEVERÁ CONTER PARTE TEÓRICA (PESQUISA) –valor 4,0
·
DEVERÁ CONTER FIGURAS ILUSTRATIVAS DO CONTEÚDO –
valor 1,0
·
EXEMPLOS DE EXERCÍCIOS RESOLVIDOS.- valor 5,0
4º bimestre
I. Geometria
métrica espacial (PESQUISAR SOBRE TODOS OS ITENS ABAIXO,NÃO DEIXE DE COLOCAR FIGURAS)
- Poliedro
- Relação de Euler
- Poliedros regulares
- Prismas
- Cubo
- Área do cubo e volume do cubo
- Paralelepípedo Retângulo
- Área do Paralelepípedo
Retângulo e volume do Paralelepípedo Retângulo
- Pirâmide
- Pirâmide de base
quadrangular
- Área e volume da Pirâmide
de base quadrangular
- Pirâmide de base hexagonal
- Área e volume da Pirâmide de base hexagonal
EXERCÍCIOS RESOLVIDOS
1)Sabendo que um poliedro possui 20 vértices e que em cada vértice se encontram 5 arestas, determine o número de faces dessa figura.
Temos que o número de vértices é igual a 20 → V = 20
As arestas que saem e chegam até o vértice são as mesmas, então devemos dividir por dois o número total de arestas.
De acordo com a relação de Euler, temos que:
F + V = A + 2
F + 20 = 50 + 2
F = 52 – 20
F = 32
F + 20 = 50 + 2
F = 52 – 20
F = 32
O poliedro em questão possui 32 faces.
2)Quantas faces, arestas e vértices possuem o poliedro chamado de Hexaedro?
O Hexaedro é o poliedro conhecido por ter 6 faces quadrangulares. Cada quadrado possui 4 vértices que recebem 3 arestas cada um.
Faces: 6
Vértices: 8
Arestas: 12
- F + V = A + 2
A = V + 6
F + V = V + 6 + 2
F + V – V = 8
F = 8
O poliedro possui 8 faces. - 3) Um prisma de base quadrangular possui volume igual a 192 cm³. Determine sua altura sabendo que ela corresponde ao triplo da medida da aresta da base.
Solução:Aresta da base: x cm
Altura: 3x cm
Volume: 192
V = x . x . 3x
3x³ = 192
x³ = 192/3
x³ = 64
x = 4
Altura: 3 . 4 = 12 cm
A altura do prisma de base é correspondente a 121 cm.4) Um prisma reto tem por base um triângulo isósceles de 8cm de base por 3cm de altura. Sabendo que a altura do prisma é igual a 1/3 do perímetro da base, calcule sua superfície total.Solução:No triângulo isósceles a altura também é mediana.i) Pela relação de Pitágoras temos:
logo a = 5cm
ii) O perímetro da base vale: 5cm + 5cm + 8cm = 18cm
iii) A altura do prisma vale
1/3 x 18 = 6cm
iv) área total
Ab = 8 x 3 /2 = 12cm²
Al = (8x6)+2 x (5x6) = 108cm²
At= 2x 12 + 108= 132cm²5) Em um prisma regular triangular, cada aresta lateral mede 10 cm e cada aresta da base mede 6 cm. Calcular desse Prisma:
a) a área de uma face lateral.
b) a área lateral.
c) a área total.
Solução:
a) Af = (6.10) cm²
Af = 60 cm²
b) A área lateral AL é a soma das áreas das três fases laterais, isto é:
AL = 3 . Af
AL = 3 . 60 cm²
AL = 180 cm²
c) A área total At é a soma da área lateral AL com duas vezes a área B de uma base, isto é:
At = AL + 2B
At = (180 + 18 √3) cm²6) Em uma piscina regular hexagonal cada aresta lateral mede 8 dm e cada aresta da base mede 4 dm. Calcule, desses prisma:
a) a área de cada face lateral;
b) a área de uma base;
c) a área lateral;
d) a área total;
Solução:
a) Af = b . h
Af = 4 .8
Af = 32 dm²
b) Ab = (6.10 √3) / 4
Ab = 24 √3 dm²
c) AL = 6.4.8
AL = 192 dm²
d) At = 2.24 √3 +192
At = 48 √3 + 192 dm² - 7)A área total de um cubo é 54 cm². Qual a medida da diagonal desse cubo?At= 6a²54 = 6a²54 /6 = a²a = √9a =3 cmdc = a√3dc = 3√3cmAssim, o cubo de área 54 cm², possui diagonal de 3√3cm8)Se a diagonal de um cubo mede √75 cm, qual a área total desse cubo?Para calcular a diagonal do cubo, utilizamos:d = a√3√75 = a√3 (fatorar o 75 que está dentro da raiz)5√3 = a√3a = (5√3) / √3a = 5 cmAt = 6a²At = 6 x 5²At = 150 cm²Logo, a área total do cubo de diagonal √75 cm é de 150 cm².9)Se a soma das arestas de um cubo é 84 cm, qual o volume do cubo?Primeiramente, é importante lembrar que o cubo possui 12 arestas, e que o volume é dado em centímetros cúbicos, logo:84 cm/12 = 7V = 73V = 343 cm3Portanto, o volume do cubo de arestas de 84 cm, é de 343 cm3.
- 10) Qual o volume de concreto utilizado na construção de uma laje de 80 centímetros de espessura em uma sala com medidas iguais a 4 metros de largura e 6 metros de comprimento?

- 11) Uma caixa de papelão será fabricada por uma indústria com as seguintes medidas: 40 cm de comprimento, 20 cm de largura e 15 cm de altura. Essa caixa irá armazenar doces na forma de um prisma com as dimensões medindo 8 cm de comprimento, 4 cm de largura e 3 cm de altura. Qual o número de doces necessários para o preenchimento total da caixa fabricada?
- Volume da caixa
V = 40 * 20 * 15
V = 12000 cm³Volume do doce
V = 8 * 4 * 3
V = 96 cm³Número total de doces armazenados na caixa
12000 / 96 = 125
Serão armazenadas 125 barras de doces na caixa com as dimensões fornecidas.




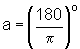 . Portanto, 1 radiano corresponde a aproximadamente 57o.
. Portanto, 1 radiano corresponde a aproximadamente 57o.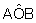 tem 1 radiano.
tem 1 radiano.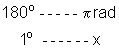
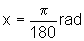 ou seja, 1o corresponde a aproximadamente a 0,017 rad.
ou seja, 1o corresponde a aproximadamente a 0,017 rad.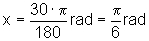
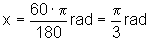
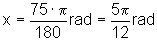
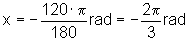
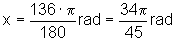
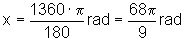
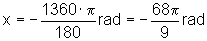
 rad,
rad, 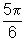 rad,
rad, 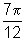 rad, 8 rad.
rad, 8 rad.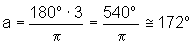
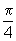 rad, temos
rad, temos 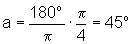
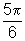 rad, temos
rad, temos 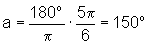
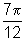 rad, temos
rad, temos 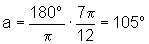
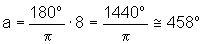
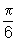 rad.
rad.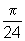 rad.
rad.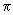 rad.
rad. rad.
rad. procurado é:
procurado é: